PROBLEMAS DE VIENTO
CON CRP-5 / E6B
LA GUÍA MÁS COMPLETA
BIENVENIDOS A BORDO
Señoras y señores, les doy la bienvenida a lo que posiblemente sea la guía más detallada y completa sobre el cálculo y resolución de problemas de viento en navegación aérea. Si has llegado hasta aquí, es muy posible que seas un alumno piloto en apuros o bien un instructor preparando la clase de mañana. Independientemente del motivo, toma asiento y prepárate para una lectura que intentaremos hacer lo más amena posible.
Esta guía ha sido diseñada para ser leída paso a paso e incluye videos explicativos. La guía pierde magia y efecto si no se visualizan los videos a medida que avanza la lectura.
¿POR QUÉ NECESITAMOS SABER RESOLVER PROBLEMAS DE VIENTO?
Aunque hoy en día existe software capaz de calcular una ruta corregida por viento en apenas segundos, resolver este tipo de ejercicios sigue siendo fundamental en la formación de futuros pilotos. A través de ellos se llegan a comprender los conceptos de heading, track, true airspeed, groundspeed, wind y velocity. Por esta razón, estos problemas siguen y seguirán formando parte de los exámenes oficiales.
VECTORES
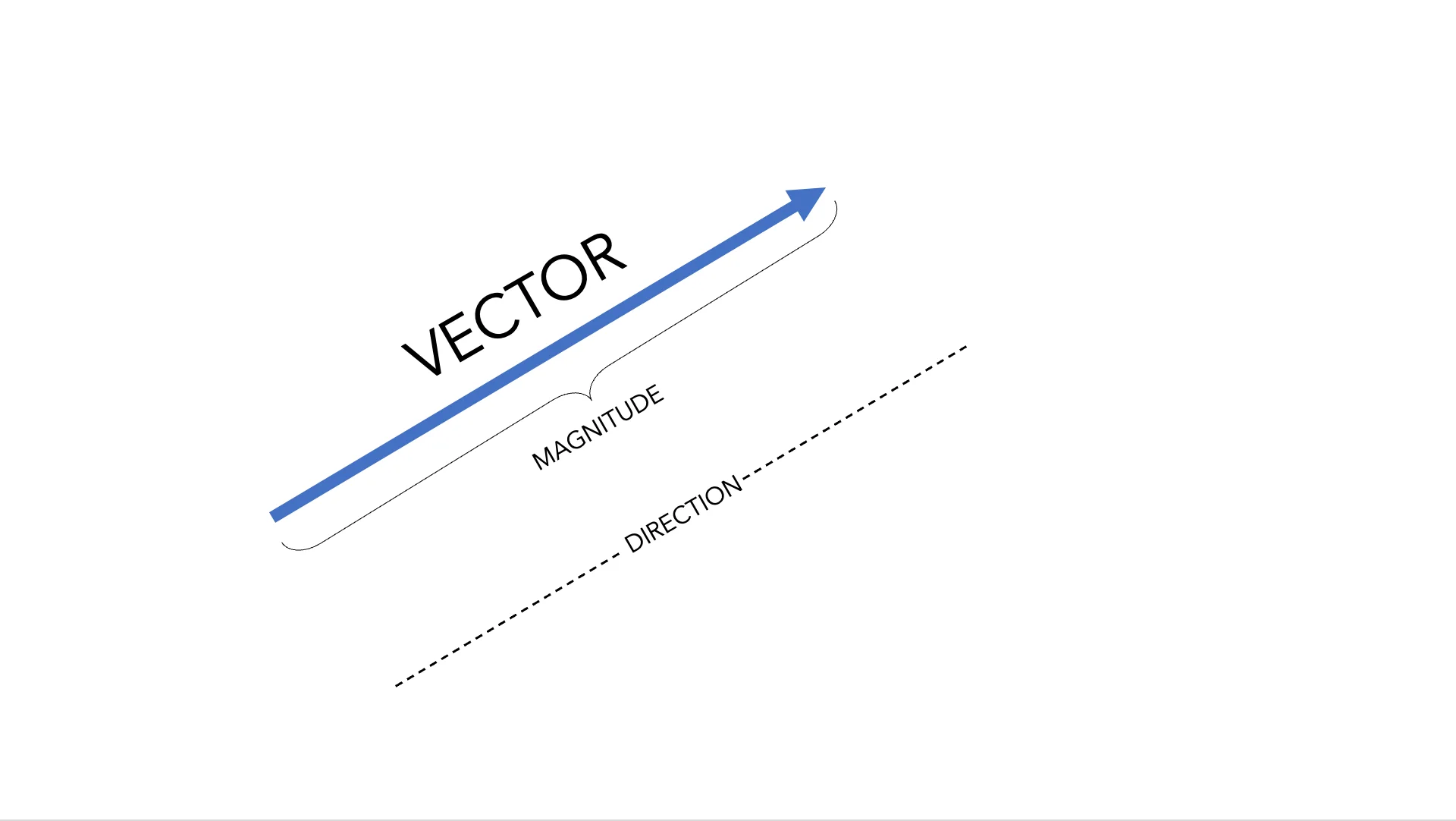
En física existen magnitudes que pueden describirse mediante un único valor y su unidad, llamadas magnitudes escalares, como por ejemplo la masa (5 kg) o la distancia (100 m). Sin embargo, otras magnitudes requieren más información para quedar completamente definidas. Un ejemplo es la velocidad. Ésta necesita un módulo (tamaño), una dirección y un sentido. Por esta razón, la velocidad es una magnitud vectorial y se representa mediante un vector.
VECTORES EN NAVEGACIÓN AÉREA
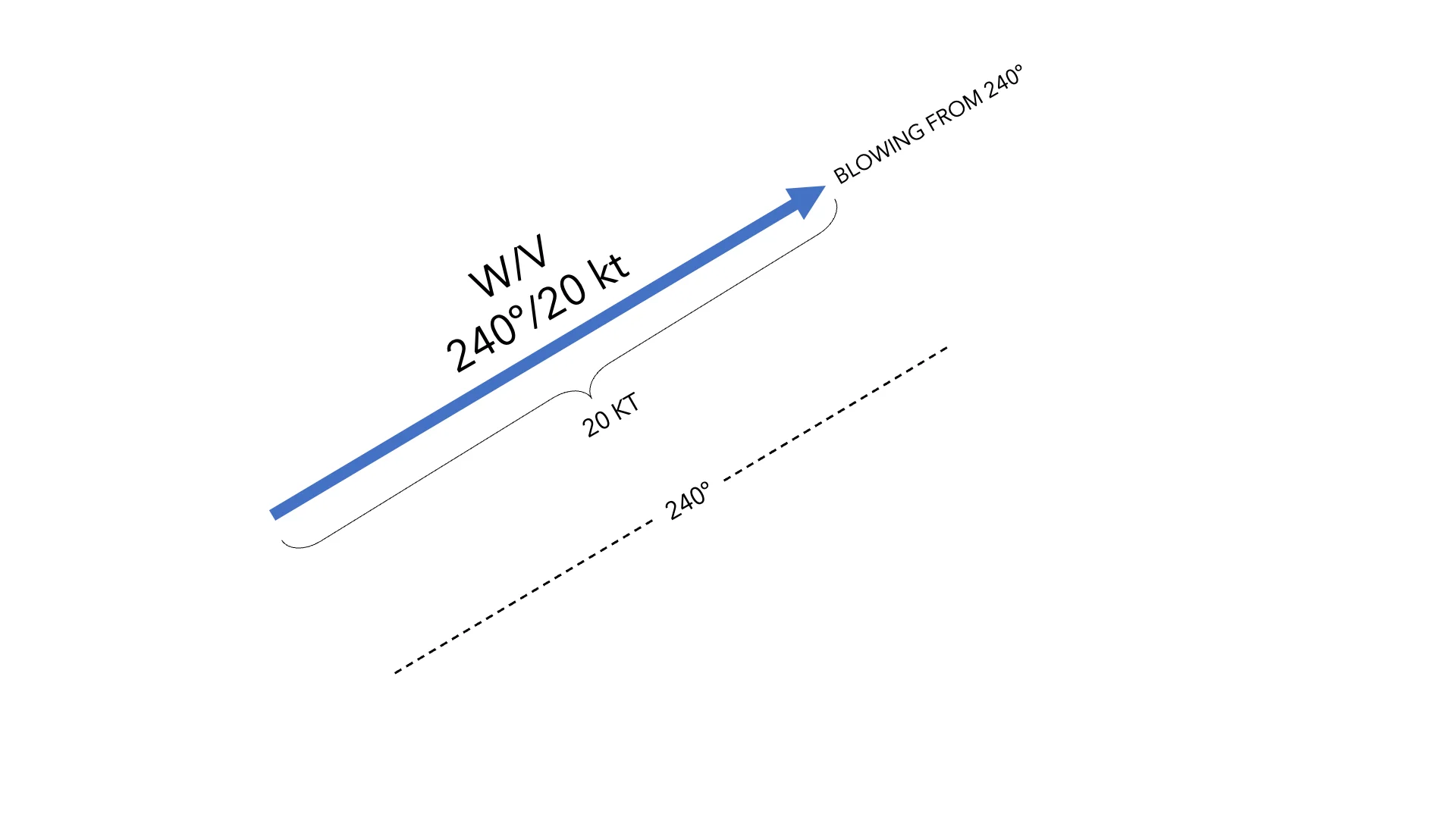
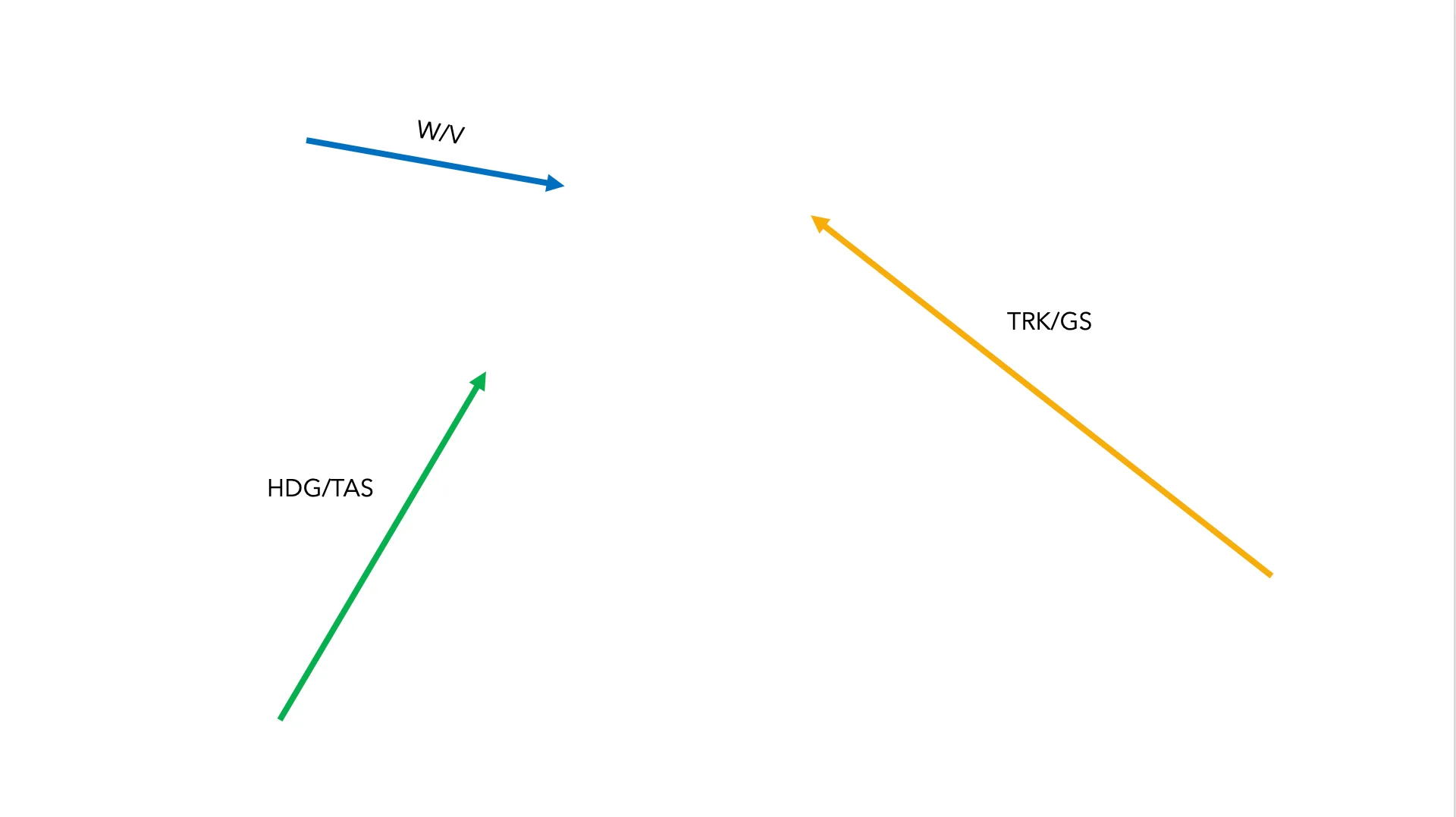
Tomemos como ejemplo el viento. No es suficiente decir que hay un viento de 20 kt, tenemos que indicar también de dónde viene ese viento para definirlo por completo. Por ejemplo, el viento viene de 240º/20kt. De esta manera tenemos definidos la dirección y sentido (sopla desde 240º) junto con el tamaño del vector viento (20 kt). Esta pareja de elementos, wind y velocity, va siempre junta para poder definir por completo el viento.
Lo mismo ocurre con la pareja de heading y true airspeed. Son dos elementos que siempre van juntos indicando donde apunta la cabeza de la aeronave y a qué velocidad se desplaza con respecto al aire.
La última pareja indivisible que nos queda es el track y la groundspeed. Estos dos elementos indican la línea que el avión vuela sobre la tierra junto con la velocidad sobre la misma. (Al track también se le conoce como course en función de si usamos inglés americano o británico).
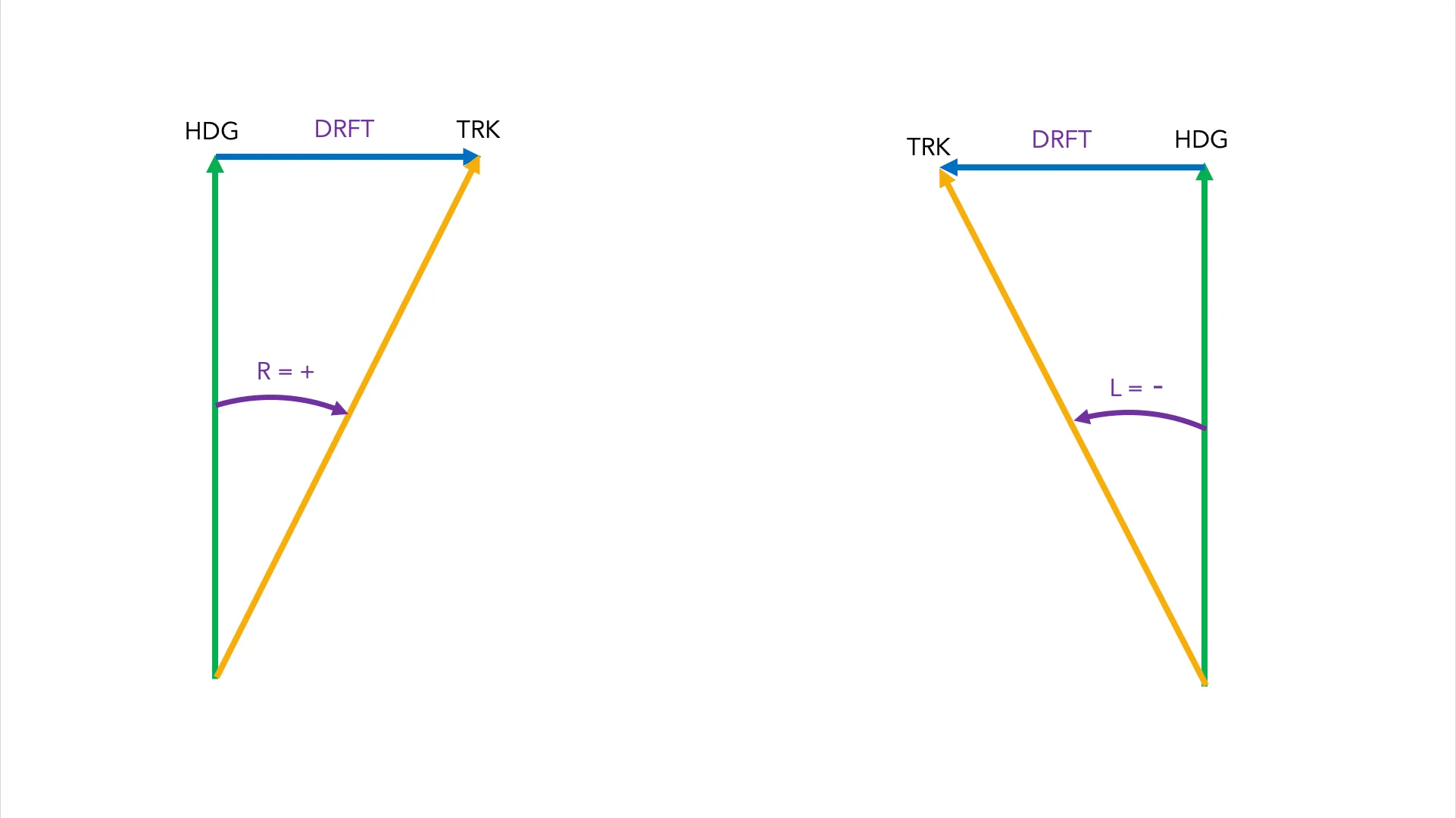
DRIFT Y WIND CORRECTION ANGLE
El drift o deriva es cuánto nos empuja el viento hacia un lado. Conceptualmente hay que pensar que el viento nos “driftea” desde nuestro HDG a nuestro TRK. Siempre en esta dirección, de nuevo y una vez más por si acaso, siempre desde nuestro HDG a nuestro TRK. Por definición el DRFT es la diferencia angular entre estos dos valores. Por ejemplo:
HDG 100º / TRK 105º —> el viento nos ha drifteado 5º a la derecha (+5º)
HDG 334º / TRK 327º —> el viento nos ha drifteado 7º a la izquierda (-7º)
El Wind Correction Angle es la corrección que deberíamos hacer para volar sobre el suelo el HDG que queríamos inicialmente. En el primer ejemplo (HDG 100º / TRK 105º) el viento nos ha drifteado 5º a la derecha (+5º) si nosotros quisiéramos compensar el viento y volar un TRK de 100º deberíamos corregir 5º hacia la izquierda (-5º) obteniendo un HDG corregido de 95º. Al volar este HDG corregido de 95º, cuando el viento nos empuje, volaremos un TRK de 100º sobre el suelo.
El DRFT y el WCA tienen el mismo valor pero signo opuesto. En todos los problemas trabajaremos siempre con DRFT. Por lo tanto, si en la pregunta nos ofrecen el WCA lo convertiremos siempre, sin pensarlo dos veces a DRFT.
SUMA DE VECTORES
Hay varias formas de sumar vectores. Una de ellas es usando matemáticas, aunque sería un proceso largo y tedioso usando papel y boli en un examen de navegación aérea. Otra opción es la suma gráfica de vectores que es mucho más visual.
Para sumar dos vectores gráficamente, se dibuja la cola del segundo vector desde la punta del primero. El vector resultante se traza desde el origen del primer vector hasta la punta del segundo. Como podéis ver en la imagen, esto resulta en un triángulo, de ahí el nombre de “triángulo de vientos”.
El CRP-5/E6B realiza exactamente una suma gráfica de vectores tal y como está descrito más arriba. Esta suma gráfica la mostramos de manera visual en el siguiente video. Disfruten de la magia (y del mago):
PROBLEMAS DE VIENTO
Los problemas de viento son siempre los mismos, nos ofrecen datos sobre dos vectores y nos piden averiguar los valores restantes. Es decir, el problema nos da 4 elementos y nos pide calcular los 2 elementos restantes. En los exémenes de navegación aérea hay tres tipos de problemas* de viento. Los vamos a clasificar de la siguiente manera:
PROBLEMA 1 - HDG/TAS, W/V —> Calcula el TRK/GS
PROBLEMA 2 - HDG/TAS, TRK/GS —> Calcula el W/V
PROBLEMA 3 - TRK/TAS, W/V —> Calcula el HDG/GS
(*Hay un cuarto problema de viento poco conocido a nivel CPL(A)/ATPL(A) que rara vez aparece en exámenes, solo apto para los más valientes: en este tipo de problema el avión vuela dos radiales VOR distintos con dos headings distintos y nos pide averiguar el W/V.)
AHORA SI, RESOLVIENDO PROBLEMAS
Es muy complejo explicar el uso del CRP-5/E6B usando solo palabras, por eso hemos creado una serie de videos explicativos resolviendo los tres tipos de problemas.
PROBLEMA 1 - HDG/TAS, W/V —> Calcula el TRK/GS
1 - Dibuja el vector W/V
2 - Coloca el center dot en la TAS
3 - Selecciona el TH girando la escala circular
4 - Lee los valores de DRFT, TRK y GS
PROBLEMA 2 - HDG/TAS, TRK/GS —> Calcula el W/V
1 - Coloca el center dot en la TAS
2 - Selecciona el TH girando la escala circular
3 - Dibuja un punto en la intersección del DRFT con en el arco de la GS.
4 - Mueve la escala circular hasta que dicho punto quede debajo en la línea de la TAS
5 - Lee el W/V
PROBLEMA 3 - TRK/TAS, W/V —> Calcula el HDG/GS
1 - Dibuja el vector W/V
2 - Coloca el center dot en la TAS
3 - Selecciona el TRK girando la escala circular
4 - Ajusta la escala circular la misma cantidad de grados a la izquierda o a la derecha que el valor de drift obtenido.
5 - Lee los valores de TH y GS
FALLOS COMUNES DE LOS ALUMNOS
Dejo una lista de errores comunes que he visto en mis alumnos a lo largo de todos estos años y que espero que vosotros nunca cometáis.
- No saber en qué tipo de problema estamos (1, 2 o 3)
- Saber en qué tipo de problema estamos pero mezclar los pasos a seguir entre varios problemas.
- Saber los pasos del problema pero completarlos en otro orden.
- A pesar de realizar bien todo lo anterior, no introducir correctamente los datos en el CRP-5.
- Confundir el center dot con el punto de la TAS que han dibujado.
- No entender el concepto de DRFT positivo o negativo, no saber cuándo sumar o restar para obtener HDG o TRK. Ante la duda lo mejor es hacerse un pequeño dibujo.
- Confundir 210º con 120º, 140º con 340º etc.
- Resolver el problema perfectamente pero leer mal el resultado.
- Mezclar unidades, por ejemplo True Heading con Magnetic Track. Antes de insertar datos en el CRP-5 asegurarnos de que todo está en True o en Magnetic.
- Poner el center dot en los números pintados en el CRP-5, no en el valor exacto. Por ejemplo, si la TAS es de 150 kt, poner el center dot en 152-154 kt.
- En el problema tipo 2 (averiguar W/V) girar la escala circular para poner el punto dibujado encima del center dot, acordarse de que es siempre debajo del center dot.
Un último consejo, probablemente el más valioso y con el que he conseguido ayudar a la mayoría de alumnos: en los exámenes oficiales encontrarás respuestas con resultados muy parecidos entre sí. Nunca, absolutamente nunca, leas las diferentes respuestas antes de resolver el problema. Al hacerlo, nuestro cerebro se sugestiona de forma inconsciente y tiende a considerar una de esas opciones como la correcta. Cuando terminamos el ejercicio y no obtenemos exactamente ninguno de los resultados propuestos, es fácil caer en el error de elegir el resultado más parecido, dejándonos llevar por esa sugestión, incluso "ajustando" el CRP-5 para que nos de ese resultado. Así que, antes de empezar el problema, NO LEAS las respuestas. Si finalmente no obtengo un resultado válido, mi recomendación es clara: paso a la siguiente pregunta y regreso más tarde para resolverla de nuevo desde cero, con la mente despejada.
ACLARACIONES PARA INSTRUCTORES Y ESCUELAS
Incluyo esta sección de aclaraciones típicas que muchos instructores me han planteado a lo largo de todos estos años.
POR QUÉ EL CRP-5 Y NO EL CR3 U OTRA CALCULADORA CIRCULAR
Dos motivos: precisión y sencillez. Siempre que el punto que dibujemos con el rotulador sea finito, el CRP-5 ofrece una precisión de +-2kt de velocidad y +-1º en las direcciones. Las calculadoras circulares como el CR3 con altas velocidades o ángulos muy pequeños por desgracia empiezan a fallar. Además, los pasos a seguir en el CRP-5 son mucho más sencillos de recordar.
POR QUÉ EL CRP-5 Y NO MATEMÁTICAS
Los vectores son herramientas matemáticas. El problema es que al 99 % de las explicaciones a las que he asistido, tanto en mi etapa de alumno como la de instructor, no se enseñaba a resolver los problemas usando vectores si no usando seno y coseno. En todas las explicaciones que he podido llegar a ver, el modus operandi consistía en descomponer el vector viento en dos componentes (viento en cara/cola y viento cruzado) para obtener el vector final. El error reside en que no se tiene en cuenta el efecto combinado del vector viento sobre la dirección del vector final resultante. En otras palabras: no se tiene en cuenta el “estiramiento” del vector final producido por la deriva. Esto, aunque parece poco importante, puede llegar bajo ciertas condiciones a dar errores de +-9 kt y +-4º, eso sin tener en cuenta los decimales que la calculadora pierde usando seno y coseno con ángulos pequeños, errores pequeños pero que van arrastrandose hasta convertirse en uno más grande.
POR QUÉ NO USAMOS LA OTRA CARA DEL CRP-5
En la otra cara del CRP-5 se puede calcular la altitud de densidad, la altitud verdadera, la TAS, el número de Mach y hacer conversión de unidades. Para realizar estas tareas sí que recomiendo encarecidamente usar fórmulas ya que en este caso, sí que van a ser más precisas que la calculadora de vuelo, además de ser más rápidos y cometer menos fallos debido a la lectura errónea de los números en la cara del CRP-5. No os preocupéis, os voy a dar todo lo necesario para que no le tengáis miedo al éxito, así que aquí van todas las fórmulas ordenadas una a una y por colores:
True Altitude = Pressure Altitude +- (Temp correction of 4% of the height for every 10º ISA dev)
Density Altitude = Pressure Altitude +- (120 x ISA deviation)
MACH = TAS / LSS (LSS = 38.95 x √273+(T) (ºC))
TAS ≈ IAS + (2% IAS every 1.000 ft altitude)
UN ÚLTIMO TRUCO DE MAGIA
Siempre me ha encantado dar clase y enseñar a mis alumnos algo valioso, ver cómo entran por la puerta con cierto pánico al CRP-5 y salen finalmente con toda la confianza al acabar la clase es una sensación indescriptible. Espero que todos vosotros os sintáis igual o al menos parecido tras esta lectura.
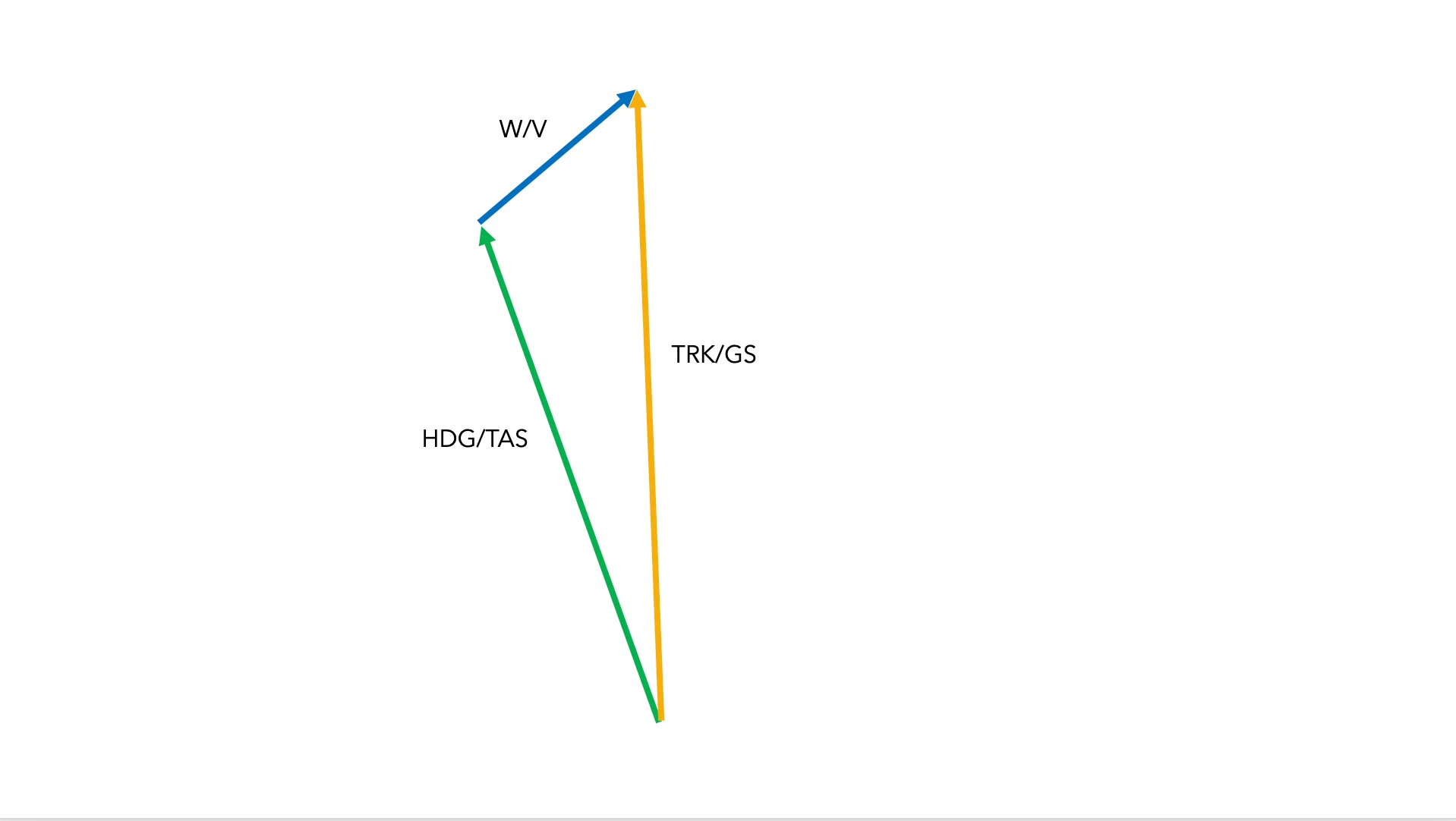
Por último, también pienso que la mejor manera de acabar cualquier clase es con un Grand Finale, un último truco de magia. Para ello, os lanzo una última pregunta:
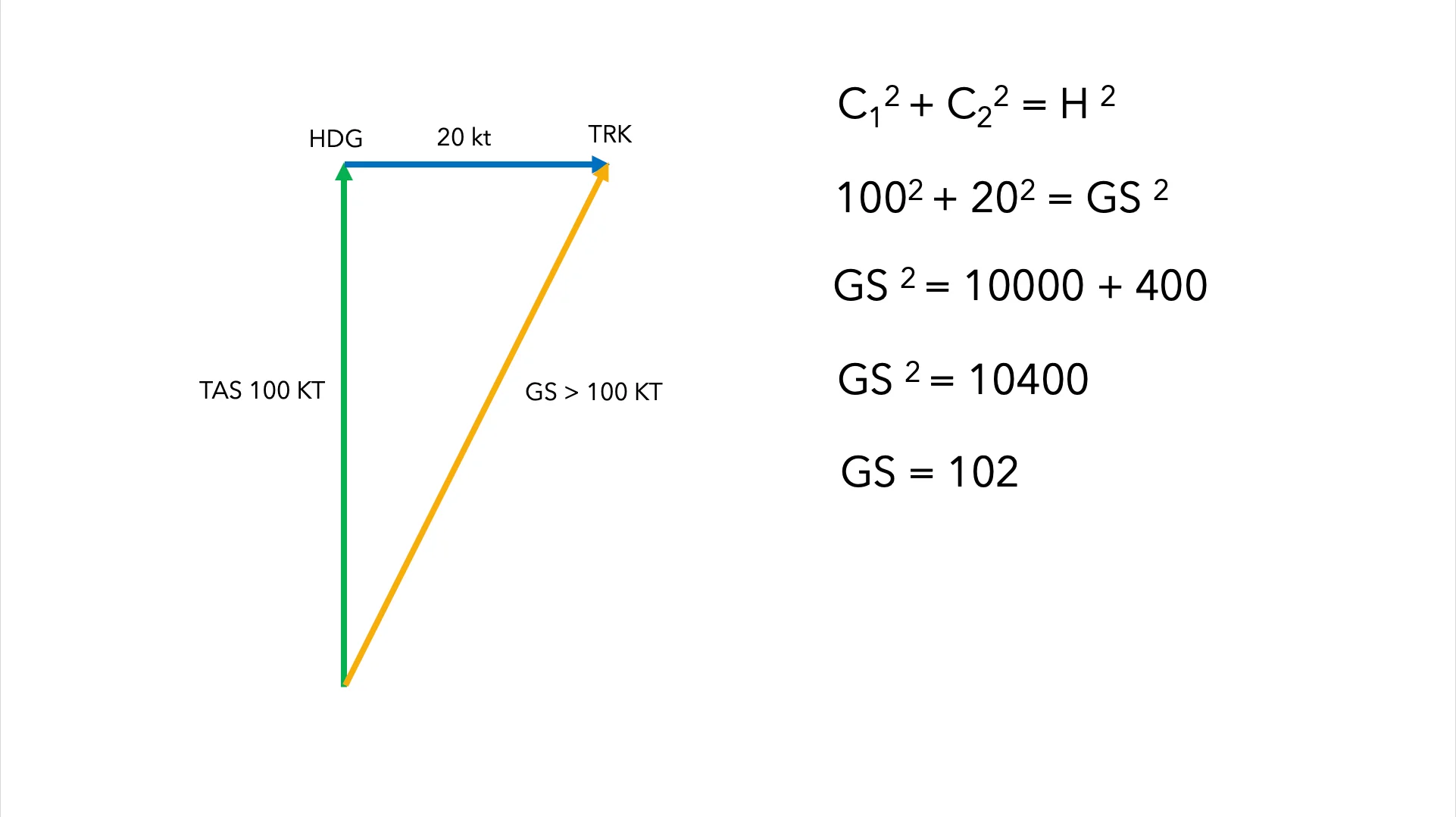
Sin usar la calculadora de vuelo. Supongamos una aeronave volando con un HDG de 360º a una TAS de 100 kt. Tenemos un viento completamente cruzado de la izquierda de 20 kt ¿Cuánto es mi groundspeed?
El 99,999 % de pilotos volando en línea aérea te dirán que la GS es igual a la TAS de 100 kt ya que el viento es totalmente cruzado, no tiene una componente en cara o en cola. Pero vosotros, queridos lectores de esta guía, como ya sabéis sumar vectores gráficamente, sois de los pocos iluminados que conocerán la verdad. Y la verdad, es que la GS es mayor a 100 kt. Y si no me crees, fíjate en este diagrama de más abajo y dime ¿no es verdad que la hipotenusa de un triángulo rectángulo es mayor a sus catetos? Un mago nunca revela sus trucos, así que os dejo reflexionar sobre este último descubrimiento.
Mi trabajo con vosotros ha terminado. Mucha suerte con vuestros exámenes, con todo nuestro cariño, el equipo de Private Pilot Exams.